最开始我以为这是个很简单的问题,结果后面我发现我看错题了………………
题目
汉诺塔(Tower of Hanoi)源于印度传说中,大梵天创造世界时造了三根金钢石柱子,其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
注意!一次只能移动一个圆盘!!
初探
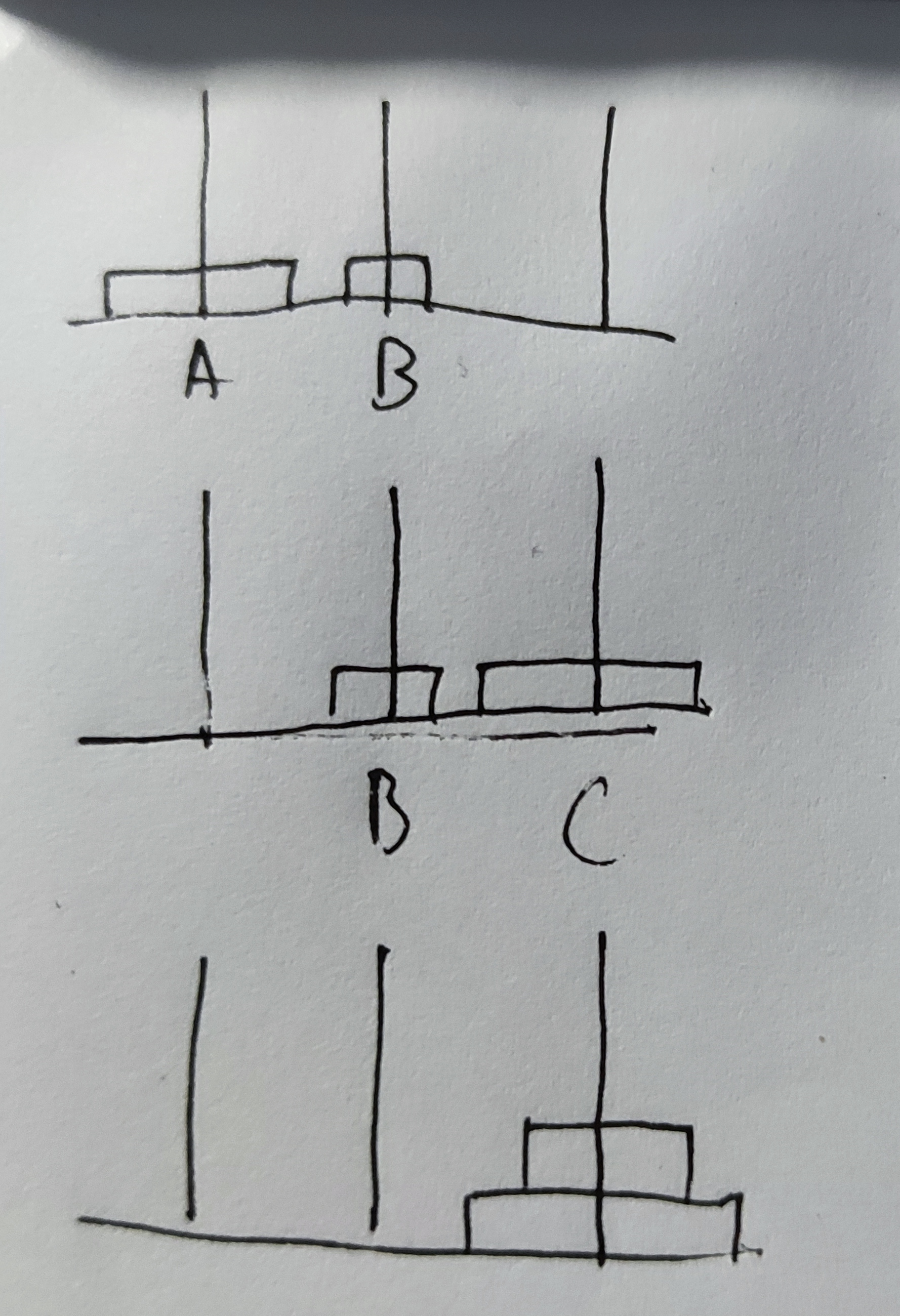
题目中,A为起始柱子,B为中间柱子,C为终到柱子
化繁为简
1阶 move(1,A,B,C)
如果只有一个片片,会怎么样?
答案很简单,A–>C,不需要以B为中转
2阶 move(2,A,B,C)
现在A有2个片了,因为大的必须要在下面,所以首要任务是把A底下的移到C去,但是小的那一个必须先动,才能移动大的。移动小的,就成了一阶的问题了,只不过,C要被大的占用,所以小片片的目标柱子成了B
所以步骤为:
1.A–>B(以A为起始,C为中间,B为目标)
move(1,A,C,B)
2.A–>C(与1阶相同)
move(1,A,B,C)
3.B–>C
move(1,B,A,C)
到此时就已经完成了
3阶
好了,现在A上有三个片片了,现在把它分开,我要把上面2个移到B上,把最大的移到C上。
应该调用什么函数?
1.move(2,A,C,B)
依照这个,让上面两个到了B,接下来,要让A剩下的最大的那个到C
2.move(1,A,B,C)
好了,最大的已经到C了,这个时候我们只需要把B上的两个到C上
3.move(2,B,A,C)
好了,结束
发现什么奇怪的东西没有??
3阶与2阶,调用的函数,除了第一步和第二步加了个1之外,都是一样的!!!
因为这时按照传统功夫 我们已经将问题化成了一个基本的递归思想!
- 将除了最大的那个其他的搬到B上
- 将最大的搬到C上
- 将B上的搬动到C上
而1与3的复杂的操作可以交给递归解决
那么函数代码可以出来了
void mover(int n, char a, char b, char c)
{
if (n == 1)
{
cout << a << "-->" << c << endl;
}
else
{
mover(n - 1, a, c, b);
cout << a << "-->" << c << endl; //这句话也可以改为“mover (1,a,b,c);”效果一样
mover(n - 1, b, a, c);
}
}
可能走得有点快了,第一次我也有点疑惑这三步为什么就可以成了?毕竟递归真的有点难以理解
递归的详解
把三阶展开来(这里之间贴知乎大佬的答案)
链接:https://www.zhihu.com/question/24385418/answer/252603808
step1. 把除了最大的盘子之外的盘子从A移到B(注意对于这个步骤来说此时A为开始柱,C为中转柱,B为目标柱,这样才能完成把最上面的2个盘子从A—>B的任务)
A—>C (开始柱—>中转柱) 【相当于调用 move(1,A,B,C)】
A—>B (开始柱—>目标柱) 【相当于调用 move(1,A,C,B)】
C—>B (中转柱—>目标柱) 【相当于调用 move(1,C,A,B)】
step2. 把最大的盘子从A移到C(对于这个步骤来说此时A为开始柱,B为中转柱,C为目标柱,这样才能把最大的盘子从A—>C)
A—>C (开始柱—>目标柱) 【相当于调用 move(1,A,B,C),即直接执行 print(’A—>C’)】
step3. 把除了最大的盘子之外的盘子从B移到C(注意对于这个步骤来说此时B为开始柱,A为中转柱,C为目标柱,这样才能完成把处于step2中的中转柱的2个盘子从B—>C的任务)
B —> A (开始柱—>中转柱) 【相当于调用 move(1,B,C,A)】
B —> C (开始柱—>目标柱) 【相当于调用 move(1,B,A,C)】
A —> C (中转柱—>目标柱) 【相当于调用 move(1,A,B,C)】
**注意到了吧,move(2,A,C,B)等价于调用 move(1,A,B,C); move(1,A,C,B); move(1,C,A,B)【注意输入的字母顺序不一样,要做相应替换!!!!】
所以函数就可以继续递归调用下去,然后完成计算。
链接:https://www.zhihu.com/question/24385418/answer/252603808
这三个步骤就是move(2,A,B,C)所做的事情,是可以详细列出每步移动的动作的。
既然最上面的2个盘子都调用move(2,A,B,C)移开了,那么第3个盘子自然也可以从A—>B了,之后再把放在C上面的2个盘子从C移动到B上就完成了移动上面3个盘子的任务了。前面的move(2,A,B,C)函数既然可以将2个盘子从A借助B移动到C并列出详细的移动动作,那么move(2,C,A,B)也就能将放在C上的2个盘子从C借助A移动到B并列出详细的移动动作,如此说来,移动3个盘子的步骤就可以总结如下了:
move(2,A,B,C)
A—>B
move(2,C,A,B)
这三个步骤就是move(3,A,C,B)所做的事情,因为我们已经证明move(2,A,B,C)和move(2,C,A,B)是可以详细列出移动2个盘子时每步移动的动作的,而中间的A—>B是一步显而易见的移动动作,所以可以确定move(3,A,C,B)是能列出每步的移动动作的。
然后根据同样的分析,最上面的3个盘子都移开了,接着只要将第4个盘子从A—>C,然后将放在B上的3个盘子移动到C上就完成全部任务了。前面我们已经证明move(3,A,C,B)能将3个盘子从A借助C移动到B并且列出详细的移动动作,那么move(3,B,A,C)也能将3个盘子从B借助A移动到C并列出每步的移动动作,这样,移动4个盘子的步骤就出来了:
move(3,A,C,B)
A—>C
move(3,B,A,C)
这三个步骤就是最开始move(4,A,B,C)函数所做的事情,因为我们已经证明move(3,A,C,B)和move(3,B,A,C)是可以详细列出移动3个盘子时每步移动的动作的,而中间的A—>C是一步显而易见的移动动作,所以可以确定move(4,A,B,C)是能列出每步的移动动作的。
需要说明的是,从xx借助xx移动到xx这样的说法在上面出现了很多次,“从”后面代表的就是开始柱,“借助”后面代表的是中转柱,“移动到”后面代表的是目标柱。你也能注意到到 开始柱,中转柱,目标柱 在不同层级下是不一样的。
代码完成
#include <iostream>
using namespace std;
void mover(int n, char a, char b, char c);
int main()
{
int m;
cout << "Input the number of disks:" << endl;
cin >> m;
mover(m, 'A', 'B', 'C');
}
void mover(int n, char a, char b, char c)
{
if (n == 1)
{
cout << a << "-->" << c << endl;
}
else
{
mover(n - 1, a, c, b);
cout << a << "-->" << c << endl;
mover(n - 1, b, a, c);
}
}
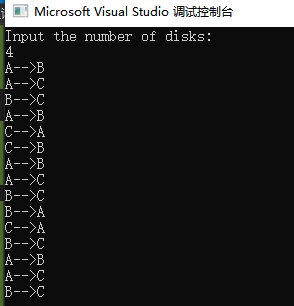
输出结果(以4阶为例)
参考链接:
https://www.zhihu.com/question/24385418/answer/252603808
https://blog.csdn.net/qq_37873310/article/details/80461767
关于递归算法,这中解决问题的方法也只有计算机才喜欢,我们虽然看着代码很简单,但真要深入理解也是很费脑细胞的,不过递归确实有中数学上的简洁美和逻辑美。
以上,Fin.