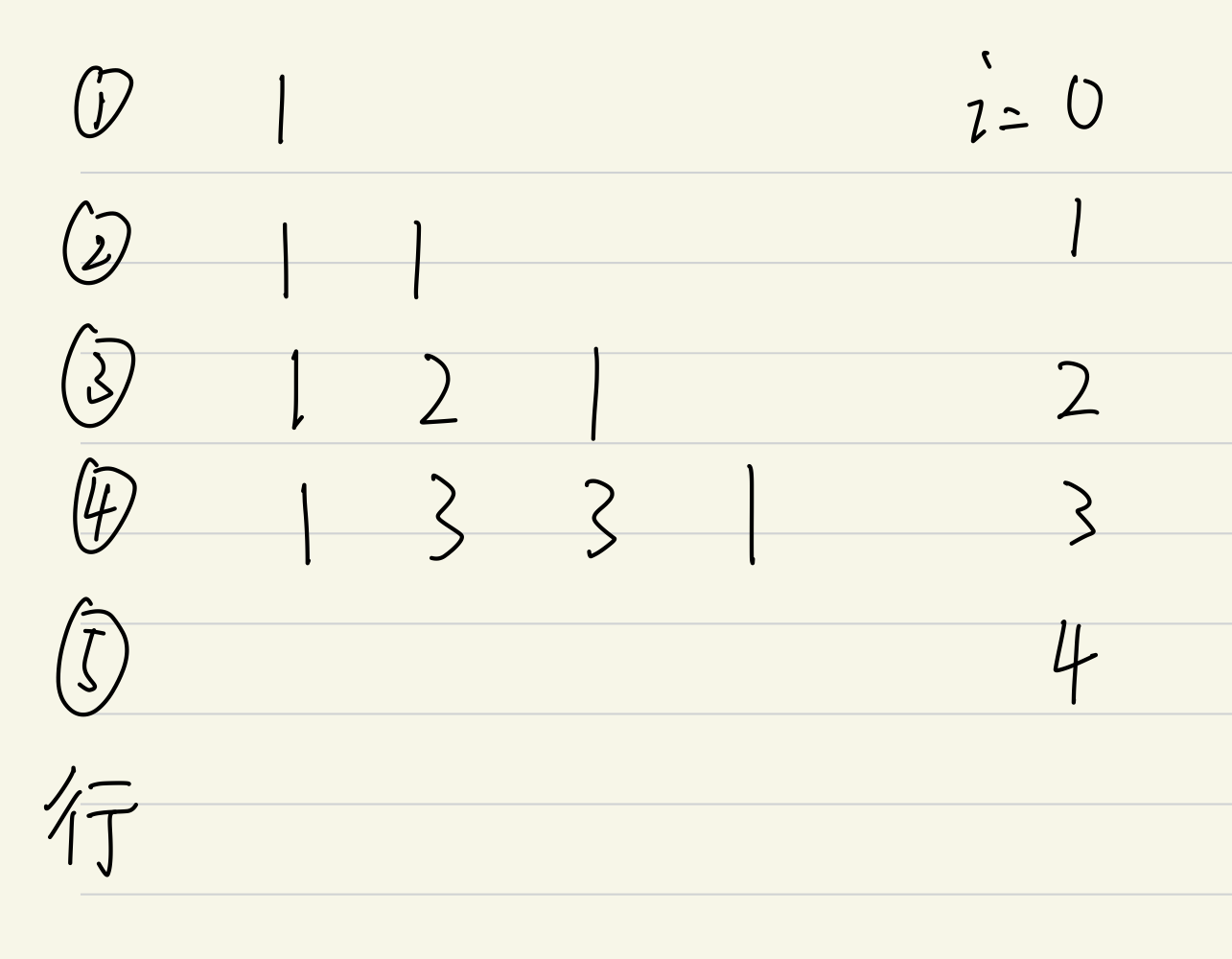动态数组-杨辉三角

浅谈一下这个有点复杂的杨辉三角

引入

二项式(a+b)^n^展开式系数由n决定，有n+1个系数

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

…………

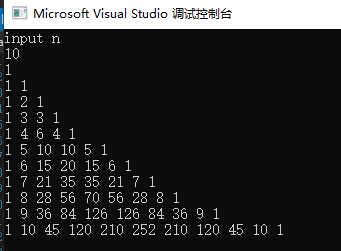
由于每行元素都是在上一行的基础上计算出来的，因此可以用一维数组进行迭代。数组长度是根据二项式的幂次决定的，所以在程序中使用动态数组。以下程序输出二项展开式 n 次幂的系数表。

书上程序

#include <iostream>
using namespace std;
void yhtriangle(int * const, int);

int main()
{
    int n, *yh;
    do
    {
        cout << "input n" << endl;
        cin >> n;
    } while (n<0||n>20);  //此段保证n处于1-19之间
    yh = new int[n + 1]; //创建n+1的数的动态数组
    yhtriangle(yh, n);
    delete[]yh;
    yh = NULL; //释放
}

void yhtriangle(int * const py, int pn)
{
    int i, j, k;
    py[0] = 1;//第一项的值为1
    cout << py[0] << endl;//0次幂的系数
    for (i = 1; i < pn + 1; i++)//依次输出n=1,2,3……到n的结果
    {
        py[i] = 1; //最后一项是1
        for (j = i - 1; j > 0; j--)
            py[j] = py[j - 1] + py[j]; //难理解句！！注意：等式右边是上一行的！左边是本行的！！
        for (k = 0; k <= i; k++)
            cout << py[k] << " "; //输出结果
        cout << endl;
    }
}

解释

最难以理解的是第28行，也就是程序的核心，那我们先从算法来看每一项是怎么来的

这就是一个杨辉三角，跟着程序走一下：

void yhtriangle(int * const py, int pn)
{
    int i, j, k;
    py[0] = 1;//第一项的值为1
    cout << py[0] << endl;//0次幂的系数

此时，数组第0项为1，第一行已经输出了

    for (i = 1; i < pn + 1; i++)//依次输出n=1,2,3……到n的结果
    {
        py[i] = 1; //最后一项是1
        for (j = i - 1; j > 0; j--)
            py[j] = py[j - 1] + py[j]; //难理解句！！注意：等式右边是上一行的！左边是本行的！！
        for (k = 0; k <= i; k++)
            cout << py[k] << " "; //输出结果
        cout << endl;
    }

进入循环，i=1，开始第二行的操作

首先将第二个数赋值1，进入循环，因为j=0，不执行循环

第二行输出，结束。

注意，结束后数组值未清空，所以我们可以利用上一行数据来算下一行！！

第3行，i=2，

第三项为1,

第二项，由第二行的第二项与第一项相加而来！！

第一项不变

第四行亦是如此

那么问题就解决啦